Converse Of Alternate Interior Angles Theorem
Converse Of Alternate Interior Angles Theorem. Converse theorem should look like "if B then A": If alternate interior angles formed by these lines are congruent [Part B] then two lines that are cut by a transversal are parallel [Part A]. Therefore, by the definition of congruent angles , We begin with the converseof the Alternate Interior Angles Theorem, as follows: If two parallel lines nand m are cut by a transversal l, then alternate interior angles are congruent.
Since k ∥ l , by the Corresponding Angles Postulate ,
They're customizable and designed to help you study and learn more effectively.
mrwadeturner / M1 Corresponding and Alternate Interior Angles
Converse of Alternate Interior Angles Theorem - GeoGebra
📈Which theorem correctly justifies why the lines m and n are parallel ...
Theorem 3 4 Alternate Interior Angles Converse | Review Home Decor
Consecutive Interior Angles Converse Theorem
mrwadeturner / Corresponding and Alternate Interior angles
Angle Properties, Postulates, and Theorems | Wyzant Resources
Alternate Interior Angles ( Read ) | Geometry | CK-12 Foundation
Proving lines are parallel
When two parallel lines are cut by a transversal, the pair of angles formed inside the parallel lines but on the opposite sides of the transversal are called alternate interior angles. Alternate Interior Angles Examples We can prove both these theorems so you can add them to your toolbox. The alternate interior angles are congruent.
Rating: 100% based on 788 ratings. 5 user reviews.
Olivia Paine
Thank you for reading this blog. If you have any query or suggestion please free leave a comment below.
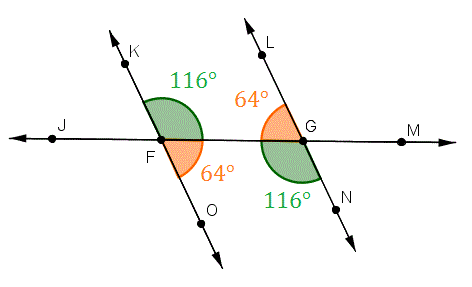
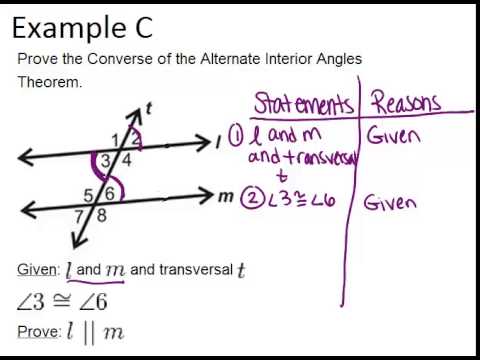
0 Response to "Converse Of Alternate Interior Angles Theorem"
Post a Comment